Leet Code笔记
- Pre
- P1 TwoSum
- P3 Longest Substring Without Repeating Characters
- P4 Median of Two Sorted Arrays
- P5 最长回文子串
- P11 Container With Most Water
- P28 字符串匹配
- P41 First Missing Positive
- P84 Largest Rectangle in Histogram
- P85 Maximal Rectangle
- P123 Best Time to Buy and Sell Stock III
- P136 Single Number
- P137 Single Number II
- P169 Majority Element
- P188 Best Time to Buy and Sell Stock IV
- P218 The Skyline Problem
- P279 Perfect Squares
- P315 Count of Smaller Numbers After Self
- P316 Remove Duplicate Letters
- P321 Create Maximum Number
- P494 求目标和
- P673 最长上升子序列个数
Pre
邪道
在题解类前面插入代码加速读取:
auto x = []()
{
std::ios::sync_with_stdio(false);
cin.tie(NULL);
return 0;
}();
浮点转整数
floor:不大于的最大整数ceil:不小于的最小整数- …
P1 TwoSum
给定一个数组,从里面挑两个使得和为某一给定值。(数不重复且每个只能挑一遍)
任意数\(A\),目标\(T\),只要\(B=T-A\)在数组内即可
为了快速验证\(B\),建立一个hash table记录索引。
for all A in Array:
if B in hash table:
return result
Add A to hash table
P3 Longest Substring Without Repeating Characters
数组\(A\)记录每个字符上一次出现的位置
记录当前不重复子串的起始位置\(l\)
l = 0
for all character C in s:
if A[C] >= l:
l = A[C] + 1
Calculate length start from index l and ends at character C
Update max length
时间复杂度\(O(n)\)
P4 Median of Two Sorted Arrays
中位数:所有小于等于中位数的个数和大于等于中位数的个数相等
数组\(A_N\)和\(B_M\),在\(A\)中找到分割点\(i\),在\(B\)中找到分割点\(j\),将整个数组分为两个部分\(L\)和\(H\):
AL = A[:i]
AH = A[i:]
BL = B[:j]
BH = B[j:]
L = AL + BL
H = AH + BH
如果能找到这样的\(i\),\(j\)使得\(L\)正好是小于中位数的那一半,而\(H\)正好是大于中位数的那一半,那么就可以找到中位数。
分成两半\(i+j=N-i+M-j\),得到\(j=0.5*(N+M)-i\)。由于两个数组本生是排好序的,所以满足中位数的条件有两个:\(A_{i-1}\le B_j\)以及\(A_i\ge B_{j-1}\)。
如果条件一不满足,说明\(i_{real}\lt i\);如果条件二不满足,说明\(i_{real}\gt i\);两个条件不可能同时不满足。
二分即可
P5 最长回文子串
首先在字符之间和首尾加上特殊符号,可以是’#’,这样就不用考虑回文串的长度的奇偶
再在新串的首位加上不同的特殊符号,可以是’^’和’$’,这样就不用单独考虑边界情况
b a b c b a b c b a c c b a
^#b#a#b#c#b#a#b#c#b#a#c#c#b#a#$
记\(P_i\)为以\(i\)为中心,最大的回文长度(距中心的长度)
0123456789ABCDEF...
^#b#a#b#c#b#a#b#c#b#a#c#c#b#a#$
P010301070109010...
定义已知回文串中心\(C\),以及其右端点\(R\)
对于字符串上的每一个位置\(i\),如果\(i\lt R\)说明该中心位于已知回文串的内部,那么根据对称性,\(P_i=P_{2*C-i}\),例如当\(C=11\),\(i=13\)时,\(P_{11}=P_9=1\);但当\(i=15\)时,如果用相同的方法,\(P_{15}=P_7=7\),就会发现\(i\)为中心的子串的右端点\(15+7=22\)超过了\(C\)为中心的子串的右端点\(R=20\),而\(R\)右侧的情况是未知的,所以最右只能取到\(R\),之后要逐项判断:
P[i]=max{min{P[2*C-i], R-i}, 0}
P[i]=Expand(P[i])
显然如果\(i\)本身就在\(R\)右侧那么就没有对称性可以参考,也必须逐项判断
如果扩展结束后的回文串的右端点超过\(R\),即\(P_i+i\gt R\),那么就把\(i\)作为新的中心,\(P_i+i\)作为新的右端点
最后把\(P\)数组遍历一遍,找到值最大的,取值和其索引,索引恢复到原始串的索引,值恢复到原始串内的长度(一半)
P11 Container With Most Water
用\(f_{i,j}\)表示左端\(i\),右端\(j\)可以存多少,\(f_{i,j}=min(h_i,h_j)*(j-i+1)\)。
理论上所有\((i,j)\)组合都要算一遍但是由于高度是短板决定的,所以
如果短板是\(i\):
\[\begin{align} f_{i,j}&\gt min(h_i, h_j)*(k-i+1)\\ &\ge min(h_i, h_k)*(k-i+1)\\ &=f_{i,k} \end{align}\]即所有以\(i\)为左端点,\(j\)左侧的点为右端点的就不用算了;短板是\(j\)时同理,\(i\)右侧的也不用算了
l = 0, r = n - 1
while l < r:
Update max area
if i is shorter:
++i
else:
--j
P28 字符串匹配
求字串在原字符串中的位置,KMP
int n = //原串长度;
int m = //子串长度;
vector<int> next_table(m, -1);// 转移表,初始-1
for(int i = 1; i < m; ++i)
{
int tmp = i - 1;// 前一个位置
while(tmp > -1)
{
tmp = next_table[tmp];// 前缀的末位索引,-1表示不存在,保持语义一致
if(needle[tmp + 1] == needle[i])
{
/* 找到i对应的前缀末位索引 */
next_table[i] = tmp + 1;
break;
}
}
}
int k = 0;
for(int i = 0; i < n;)
{
/* 一直匹配上 */
while(needle[k] == haystack[i + k] && k < m)
{
++k;
}
/* 直到末尾 */
if(k == m)
{
return i;
}
/* 如果不是末尾,找跳转表 */
if(k > 0)
{
i += k;
k = next_table[k - 1] + 1;
i -= k;
}
else
{
i += 1;
}
}
return -1;
P41 First Missing Positive
给定数组,找到最小缺失的整数
不缺的情况下\(A_i=i+1\),所以只要把每个数放到其应该出现的位置。注意点:
- 跳过不该出现的数(非正整数,超过数组大小)
- 跳过已经在正确位置上的数
- 交换过来的数可能依然不在其正确位置上,所以要持续交换直到其应该被跳过
- 数组里的数可能重复,所以如果交换的两个数相等也要跳过,防止死循环
for k, v in A:
while (v in range) and (v not in the right place) and (A[v - 1] != v):
swap(A[v - 1], A[k])
for k, v in A:
if v != k + 1:
return k + 1
P84 Largest Rectangle in Histogram
用\(f_i\)表示以\(i\)为最短两边扩展的最大面积,所以要在\(i\)左右各找到第一个比\(i\)短的。维护一个栈,顺序遍历每个长条:如果当前\(r\)比栈顶\(i\)长就直接压栈;如果当前比栈顶短:
- 弹栈得到\(i\)
- 新栈顶\(l\)必然是\(i\)左侧第一个比\(i\)短的,因为比\(i\)长的已经弹栈了
- 而当前\(r\)必然是\(i\)右侧第一个比\(i\)短的,遍历顺序就是从左往右的
- 用\(l\)和\(r\)可以计算\(f_i\)
- 挑选所有\(f_i\)里最大的为最终结果
P85 Maximal Rectangle
逐行做,\(f_i\)代表前\(i\)行的最大面积,每行都能化简成一个P84的子问题:
height = []
Set hea all to zero
for each row from top to bottom:
for each col in this row:
if value at (row, col) is 1:
++height[col]
else:
height[col] = 0
Solve P84 on height
Update max area
P123 Best Time to Buy and Sell Stock III
给出每天的股价,顺序的买入卖出记为一笔完整交易,最多\(2\)次,求最大收益。
令\(A_{i,j}\)、\(B_{i,j}\)、\(P_i\)分别表示第\(i\)天(\(1\)开始计数)完成\(j\)次(\(1\)开始计数)买入时的最优收益、完成\(j\)次卖出时的最优收益、股价。那么:
- 第\(i\)天可以正好买第\(j\)笔(\(B_{i-1,j-1}-P_i\)),也可以之前就买了第\(j\)笔但一直没卖出(\(A_{i-1,j}\)),所以有\(A_{i,j}=max(B_{i-1,j-1}-P_i,A_{i-1,j})\)
- 第\(i\)天可以正好卖第\(j\)笔(\(A_{i-1,j}+P_i\)),也可以之前就卖了第\(j\)笔但一直没进行下一次买入(\(B_{i-1,j}\)),所以有\(B_{i,j}=max(A_{i-1,j}+P_i,B_{i-1,j})\)
买入收益必为负,所以初始条件\(A_i=(-\inf,-\inf)\);而卖出收益至少为\(0\),所以初始条件\(B_i=(0,0)\)。由于条件为“至多”所以诸如\(A_{1,2}\),\(B_{2,2}\)之类的交易是存在的,假装在第\(0\)天进行了任意次无实际意义的虚交易即可。
DP方程:
\[\begin{align} A_{i,j}&=max(B_{i-1,j-1}-P_i,A_{i-1,j})\\ B_{i,j}&=max(A_{i-1,j}+P_i,B_{i-1,j})\\ result&=B_{n,k} \end{align}\]A = [-INT_MAX, -INT_MAX, -INT_MAX] * (n + 1)
B = [0, 0, 0] * (n + 1)
for each i, price:
for j in [1, 2]:
A[i][j] = max(A[i - 1][j], B[i - 1][j - 1] - price)
B[i][j] = max(B[i - 1][j], A[i - 1][j] + price)
return B[n][2]
优化
- 虚交易不止可以在第\(0\)天做,任意一天同时进行买入卖出相当于跳过了一次交易
- DP结果每一行都只和上一行有关,空间上可以消掉一维
允许当天卖掉同时买进,修改\(A\)的转移方程,第\(i\)天买入第\(j\)笔的时候允许在同一天卖掉第\(j-1\)笔,相当于第\(j-1\)笔的买入就是第\(j\)笔的买入,第\(j-1\)笔交易被跳过。也可以修改\(B\)的转移方程,允许第\(j\)笔买入的同一天卖出第\(j\)笔,相当于跳过了第\(j\)笔。
\[\begin{align} A_{i,j}=max(B_{i-1,j-1}-P_i,A_{i-1,j})&\rightarrow A_{i,j}=max(B_{i,j-1}-P_i,A_{i-1,j})\\ B_{i,j}=max(A_{i-1,j}+P_i,B_{i-1,j})&\rightarrow B_{i,j}=max(A_{i,j}+P_i,B_{i-1,j})\\ result&=B_{n,k} \end{align}\]消除行与行之间的空间依赖性,保证每一列的数据在更新前一定会被使用完毕。最终的DP方程:
\[\begin{align} A_j&=max(B_{j-1}-P_i,A_j)\\ B_j&=max(A_j+P_i,B_j)\\ result&=B_{k} \end{align}\]A = [-INT_MAX, -INT_MAX, -INT_MAX]
B = [0, 0, 0]
for each price:
for j in [1, 2]:
A[j] = max(A[j], B[j - 1] - price)
B[j] = max(B[j], A[j] + price)
return B[2]
P136 Single Number
一个数组,每个数出现两遍,只有一个只出现一遍,找出这个数
因为\(A\oplus A=0\),\(0\oplus A=A\),所以把所有数异或起来,出现两遍的都消掉了,最终结果就是只出现一遍的那个数
P137 Single Number II
一个数组,每个数出现三遍,只有一个只出现一遍,找出这个数
一个数如果出现三遍,那么每一个bit上为1的次数就是3。除外那个单独的数,对所有数进行统计,每一个bit上1出现的次数一定是3的倍数。算上单独的数后,就会使得有些bit上1出现的次数为\(3k+1\),找到这些bit置为1,其余bit置为0,其表示的数就是剩下单独的数。用2bit的三进制加法器实现:\(C\)表示进位\(S\)表示个位,\(A\)表示加数位
| C | S | A | -> | C’ | S’ |
|---|---|---|---|---|---|
| 0 | 0 | 0 | -> | 0 | 0 |
| 0 | 0 | 1 | -> | 0 | 1 |
| 0 | 1 | 0 | -> | 0 | 1 |
| 0 | 1 | 1 | -> | 1 | 0 |
| 1 | 0 | 0 | -> | 1 | 0 |
| 1 | 0 | 1 | -> | 0 | 0 |
| 1 | 1 | 0 | -> | X | X |
| 1 | 1 | 1 | -> | X | X |
得到:
\[\begin{align} S'&=\bar{C}\land(S\oplus A)\\ C'&=\bar{S'}\land(C\oplus A) \end{align}\]最终\(S\)即要求的数
推广到每个数出现\(k\)遍,用\(log_2{k}\)个bit实现\(k\)进制加法器,最后个位数为最终结果。
P169 Majority Element
一个数组\(A\)内有且仅有一个数的数量严格超过数组大小的一半,找到这个数
记录一个潜在的众数\(cur\leftarrow A_0\)以及该数被统计的次数\(cnt\leftarrow 1\)
对于数组内的每一个数\(A_i\):
- 如果\(cur=A_i\),则\(cur\)可能是最终结果也可能不是,计入统计待定:\(cnt\leftarrow cnt+1\)
- 如果\(cur\neq A_i\),则\(cur\)和\(A_i\)当中至多只有一个是最终结果,由于最终结果的数量大于总数的一半,可以直接从数组中删除这两个数,对于剩下的部分
- \(res\gt n/2\gt(n-2)/2\),两个数都不是结果
- \(res-1\gt n/2-1=(n-2)/2\),其中有一个是结果
- 因此新数组上的解就是原数组上的解
- 由于\(cur\)被删除一个,更新统计计数\(cnt\leftarrow cnt-1\)
- 当\(cnt\)被减到\(0\)时,说明之前统计的数已经被删完了,根据之前的结论,数组剩余部分的解就是原始数组的解,重新开始新一轮求解\(cur\leftarrow {A'}_0\)以及\(cnt\leftarrow 1\)
当所有数处理完之后,剩下的没办法删除的数(\(cur\))就是最终结果
P188 Best Time to Buy and Sell Stock IV
是P123 Best Time to Buy and Sell Stock III的扩展版,将\(2\)扩展为\(k\),但是存在以下优化:如果交易数量足够保证每天都可以进行交易,那么就可以不考虑交易次数的限制,问题简化为不限次数的最优解。
令\(A_i\)、\(B_i\)、\(P_i\)分别表示第\(i\)天买入时的最优收益、卖出时的最优收益、股价。那么:
- 如果第\(i\)天买入,那么可以选择真实买入\(B_{i-1}-P_i\),也可以虚交易\(A_{i-1}\):\(A_i=max(A_{i-1}, B_{i-1}-P_i)\)
- 如果第\(i\)天卖出,那么可以选择真实卖出\(A_{i-1}+P_i\),也可以虚交易\(B_{i-1}\):\(B_i=max(B_{i-1}, A_{i-1}+P_i)\)
同样进行虚交易和空间优化,得到:
\[\begin{align} A&=max(B-P_i,A)\\ B&=max(A+P_i,B)\\ result&=B \end{align}\]A = -INT_MAX
B = 0
for each price:
A = max(A, B - price)
B = max(B, A + price)
return B
剪枝之后\(O(kn)\)的DP就优化成了\(O(n)\)的DP,在\(k\)较大的时候性能提升明显
P218 The Skyline Problem
给定一串底部紧贴x轴的矩形,求这些矩形覆盖的2D区域上外轮廓中水平线的左顶点坐标。
每个矩形有左右两个点\(p_l(l,h),p_r(r,-h)\)。右顶点的高度取反一是为了排序,二是为了区分左右顶点。排序先按x坐标小到大,x坐标相同则按y坐标大到小。
所有\(p_l\)都在水平线左侧,因而都是潜在的目标点,而所有\(p_r\)虽然在水平线右侧但是可能切割其它水平线产生目标点。
维护一个大根堆,记录访问过\(p_l\)但是还没访问过\(p_r\)的矩形高度,堆用来获取最大高度
逐顶点顺序操作:
- 如果访问到\({p_i}_l\),其为潜在目标点,因而需要判断其是否会被挡住,显然,如果新矩形高于堆顶的高度(\(\gt\)),则没被挡住,\({p_i}_l\)确认为下一个目标点;反之就不是目标点。无论其是不是目标点,该矩形已经被处理完毕,插入堆中。
- 如果访问到\({p_i}_r\),其可能生成目标点,如果矩形\(i\)是最高的矩形(没有之一),假设次高的矩形为\(j\)(可以之一),那么必然会产生一个目标点\(p({p_i}_r.x, {p_j}_l.y)\),其意义为:最高的矩形结束前,次高矩形被遮挡,而最高矩形结束后,次高矩形不再被遮挡,因而次高矩形的水平线被分为两部分,分割点为未被遮挡的水平线左端点,即目标点。反之,如果其不是最高矩形,其本身就被遮挡,没有能力切割最高的水平线,因而不会生成目标点。
为什么右顶点高度取反,为什么高度从大到小。考虑两个顶点x坐标相同
左左情形:如果先处理低的,只要低的没被挡住,高的也不会被挡住,就会同一个x出现两个目标点;而如果先处理高的,低的一定会被高的挡住,所以最多出现一个目标点。
左右情形:如果先处理右,右顶点处理完后就离堆了,所以左右顶点之间没有联系,因而就可能出现两个目标点;而如果先处理左,只要左顶点在堆内最高成为了目标点,右顶点一定不是堆内最高的矩形的,所以会被遮挡,所以最多出现一个目标点。
右右情形:如果先处理高的,显然只要高的是最高的,低的是次高的,就会生成两个目标点(高切割低,低切割其它),而如果先处理低的,其一定会被高的遮挡,所以最多也出现一个目标点。
综上所述,右顶点高度取反然后按高度值从大到小排序完美符合要求
为什么当前顶点对应的矩形一定要是高度最高的(用\(\gt\)判断)才会作为或生成目标点
考虑仅有两个高度相同且重叠的矩形[l=1, r=3, h=2],[l=2, r=4, h=2]:
如果左顶点用\(\geq\),(2, 2)就会成为一个目标点
如果右顶点用\(\geq\),(3, 2)就会被切割为一个目标点
最终结果就会变成[(1, 2), (2, 2), (3, 2), (4, 0)],而不是[(1, 2), (4, 0)]
P279 Perfect Squares
一个正整数,分解成完全平方数的和,求最少能分解成几个。
参考拉格朗日四平方定理,每一个正整数都可以表示为四个整数的平方和。所以解只有4种:\(1,2,3,4\)
参考勒让德三平方定理,形如\(4^p(8q+7)\)的正整数,其解必然是4,其余的正整数,其解之多为3。
所以先除以因数\(4^p\),剩余部分模8,余数为7的其解就是4。剩下的判断能否由2个完全平方数表示(一个可以表示为\(0^2+a^2\),所以只剩下2和3两种情况)。如果能就是2(或1),如果不能就是3。
P315 Count of Smaller Numbers After Self
给定一个序列,求每个数右边所有小于它的数的个数。
先遍历一遍确认所有数的范围。建立线段树,每个节点记录该区间内的数的数量。
上面的线段树很稀疏,所以可以压缩:先排序,然后按从小到大编号,相同数字编号相同(如\(5,2,6,1\)编号为\(2,1,3,0\)),这样就可以把原数列压缩成0开始的连续整数。
新的数正好当作索引,建立BIT。对于每个数\(x\),首先获取编号\(i=f(x)\),然后BIT查找\(BITSum(i)\),随后把这个数插入树中\(BITAdd(i+1)\)
def BITSum(i):
while i > 0:
sum += BIT[i]
i = i - (i & -i)
def BITAdd(i, v):
while i < n:
BIT[i] += v
i = i + (i & -i)
P316 Remove Duplicate Letters
给定一个字符串,去掉重复字符,使得剩下的按字典序排序最小。
对每个字符按顺序处理,同时统计每个字符剩余数量以及每个字符是否被使用:
- 找到第一个没有用过的字符,如果比栈顶字符大,直接入栈。
- 如果比栈顶字符小,检查能否去掉栈顶字符。
- 如果栈顶字符还有剩余,就弹栈,并重复2。
- 如果栈顶字符没有剩余,栈里的已经是最优了,不动。
- 将新字符入栈。
P321 Create Maximum Number
给两个数组\(a,b\),从里面取共\(k\)个数字使得拼出来的数最大,从同一个数组里取出的数顺序要不变。
- 分\(k+1\)种情况讨论:\([0,k],[1,k-1],...,[k,0]\),每种情况如何挑出目标数量的数可以用栈实现(P316)。
- 然后从挑出来的两组数中拼出最大数。
每次从两个数组开头各取一个数\(a_i,b_j\),分以下几种情况讨论:
- \(a_i\gt b_j\):选择\(a_i\),且\(i\leftarrow i+1\)
- \(a_i\lt b_j\):选择\(b_j\),且\(j\leftarrow j+1\)
- \(a_i=b_j,a_{i+1}\gt b_{j+1}\):选择\(a_i\),且\(i\leftarrow i+1\)
- \(a_i=b_j,a_{i+1}\lt b_{j+1}\):选择\(b_j\),且\(j\leftarrow j+1\)
- \(a_i=b_j,a_{i+1}=b_{j+1}\):进一步分类
进一步讨论第5种情况。
该情况下,我们有两种选择方案,仅从单一数组取(下图左,由于选\(a\)还是选\(b\)是一样的,不妨选\(b\)),以及从两个数组取(下图右)。

为了区分这两种情况,引入一个分割点\(sp\)(下图左)。同时为了进一步确认应该选择哪种情况,需要记录两个数组的起始位置\(ii\)和\(jj\),然后处理下一组数据(下图右)。有了上述描述,就可以具体表示两个分支:
- 起始\(b_{jj}\),中止\(b_{j}\)
- 起始\(b_{jj}\),中止\(b_{sp}\);接上起始\(a_{ii}\),中止\(a_{j-1-sp+ii}\)
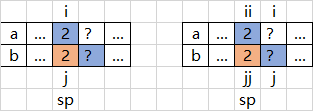
根据两个分支的中止值\(b_{j}\)以及\(a_{j-1-sp+ii}\)的大小关系可以分成三种情况:
情况5-1:\(b_{j}\lt a_{j-1-sp+ii}\)

如上图所示,最优解是\(2,2\),所以任意取走一个,问题退化为情况1(或2)。
情况5-2:\(b_{j}\gt a_{j-1-sp+ii}\)
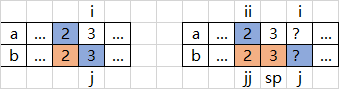
如上图所示,最优解是\(2,3\),但无法确认是取数组\(a\)还是数组\(b\),问题退化为情况3或4或5
情况5-3:\(b_{j}=a_{j-1-sp+ii}\)
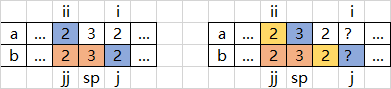
例子:

P494 求目标和
给定\(n\)个数\(x_1,x_2,...,x_n\)以及目标数\(s\),为每个数分别取系数\(k_1,k_2,...,k_n\),其中\(k_i=\{-1,1\}\),使得\(\sum{k_i x_i}=s\),求满足条件的系数序列\(k_1,k_2,...,k_n\)的个数
- DP:\(f_{i,j}\),表示前\(i\)个数字,和为\(j\)的种数。对于第\(i+1\)个数,要么取正,要么取负。所以\(f_{i+1,j}=f_{i,j-x_{i+1}}+f_{i,j+x_{i+1}}\),最终结果为\(f_{n,s}\)
- 改进DP:
- 假设所有数之和为\(S\),那么全取正得到最大值\(S\),全取负得到最小值\(-S\)。目标方程可以变为\(\sum{k_i x_i}=s+S\),其中\(k_i=\{0,2\}\)
- 上述变化之后,由于系数\(k_i\)是偶数,所以等号右侧也是偶数,目标方程进一步变为\(\sum{k_i x_i}=(s+S)/2\),其中\(k_i=\{0,1\}\)
- 还是用\(f_{i,j}\)表示前\(i\)个数字,和为\(j\)的种数。对于第\(i+1\)个数,要么取,要么不取。所以\(f_{i+1,j}=f_{i,j}+f_{i,j-x_{i+1}}\)
- 上式中\(i\)的空间是可以优化掉的,只要循环时\(j\)倒序:\(f_j=f_j+f_{j-x_{i+1}}\),最终结果为\(f_{(s+S)/2}\)
P673 最长上升子序列个数
- \(l_i\)为以\(s_i\)作为初始字符的LIS长度
- \(n_i\)为以\(s_i\)作为初始字符的LIS个数
但是最终结果不限定初始字符的位置,所以要遍历\(l_i\)
\[L=max\{l_i\}\] \[N=\sum_{l_i=L}{n_i}\]